Subsections
Default file names and directories
For some applications, the HEALPix facilities
require some precalculated input files describing the pixel window
function and ring-based or pixel-based quadrature weights (shipped as
Healpix/data/pixel_window_n????.fits,
Healpix/data/weight_ring_n?????.fits and
Healpix/data/weight_pixel_n?????.fits respectively).
By default, files with the very same name (generated by functions such as
get_healpix_pixel_window_file)
will be looked for into a list of directories (generated by
get_healpix_data_dir)
containing the current directory (.), the parent directory (..),
./data, ../data, $HEALPIX and $HEALPIX/data where $HEALPIX is
a system variable defined as the full path to the HEALPix package
(see the installation documentation).
However, the user has the possibility to change both the name of those files
and their location (with options like
windowfile,
winfiledir,
w8file, or
w8filedir)
Double/Single precision mode
Several facilities offer the option of switching at run time
the precision of the internal variables and arrays and of the I/O data from single to double precision
floating point reals. The following points should be noted:
- Facilities running in double precision mode can read indifferently single and double
precision data files (and the same is true for single precision facilities). On
the other hand, a double (resp. single) precision facility will only output double
(single) precision files.
- Since the internal calculations sensitive to numerical round-off error
(like the spherical harmonics recurrence) are
always performed in double precision, switching to double precision mode
- will have a limited impact on the output accuracy if the input file contains only
single precision data,
- is recommended if the input file contains double precision data, and the precision of the output is critical
- will only increase a bit the execution time (by 15% in some of our tests), but
it will almost double the memory consumption of the facility,
- will obviously double the size of the output file(s).
Beam window function files
Several F90 and IDL applications (eg,
alteralm,
sky_ng_sim,
smoothing,
synfast,
ialteralm,
ismoothing,
isynfast)
accept, generally with the argument beam_file a circular (possibly non-gaussian) beam or smoothing window,
which is described under the form of its real (polarized) Legendre window functions
(see IDL's beam2bl)
read from an external file.The file is either
- highly recommended: a FITS file containing a binary or ASCII table, with 1, 2 or 3 fields, respectively
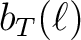 , [
, [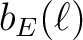 , [
, [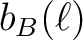 ]]
]]
- in IDL, is can also be an array of size (
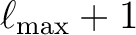 ,d) with d=1, 2 or 3, which will be
automatically turned into a FITS file of the format described above using the
HEALPix/IDL routine bl2fits.
,d) with d=1, 2 or 3, which will be
automatically turned into a FITS file of the format described above using the
HEALPix/IDL routine bl2fits.
- or, it can also be, a plain text file with 2, 3 or 4 columns, containing, on each line,
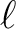 ,
, 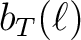 , [
, [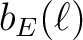 , [
, [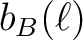 ]]
]]
and in which lines starting with a # sign are ignored.
In any case,
the multipole 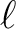 must take all integer values in
must take all integer values in
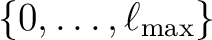 ,
with the assumption that the window functions vanish outside that range.
bT is the 'temperature' or intensity window function,
while the optional bE and bB are respectively the electric (or gradient) and
magnetic (or curl) components of polarization.
If not provided,
,
with the assumption that the window functions vanish outside that range.
bT is the 'temperature' or intensity window function,
while the optional bE and bB are respectively the electric (or gradient) and
magnetic (or curl) components of polarization.
If not provided, 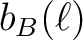 takes the value of
takes the value of 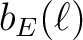 which itself defaults to
which itself defaults to 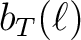 .
With these window functions, the (polarized)
map spherical harmonics coefficients and its power spectra are transformed according to
.
With these window functions, the (polarized)
map spherical harmonics coefficients and its power spectra are transformed according to
with
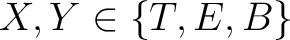 .
.
Version 3.83, 2024-11-13
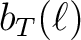 , [
, [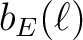 , [
, [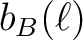 ]]
]]
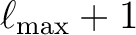 ,d) with d=1, 2 or 3, which will be
automatically turned into a FITS file of the format described above using the
HEALPix/IDL routine bl2fits.
,d) with d=1, 2 or 3, which will be
automatically turned into a FITS file of the format described above using the
HEALPix/IDL routine bl2fits.
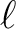 ,
, 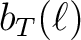 , [
, [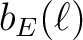 , [
, [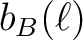 ]]
]]
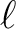 must take all integer values in
must take all integer values in
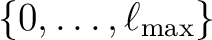 ,
with the assumption that the window functions vanish outside that range.
bT is the 'temperature' or intensity window function,
while the optional bE and bB are respectively the electric (or gradient) and
magnetic (or curl) components of polarization.
If not provided,
,
with the assumption that the window functions vanish outside that range.
bT is the 'temperature' or intensity window function,
while the optional bE and bB are respectively the electric (or gradient) and
magnetic (or curl) components of polarization.
If not provided, 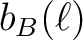 takes the value of
takes the value of 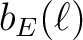 which itself defaults to
which itself defaults to 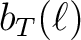 .
With these window functions, the (polarized)
map spherical harmonics coefficients and its power spectra are transformed according to
.
With these window functions, the (polarized)
map spherical harmonics coefficients and its power spectra are transformed according to
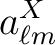
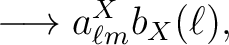
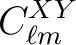
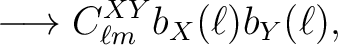
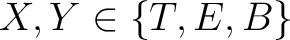 .
.