Previous: map2alm_iterative* Up: HEALPix Fortran90 Subroutines Overview Next: maskborder_nest Top: Main Page
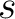 and
and 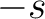 .
A (complex) map
.
A (complex) map 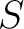 of spin
of spin 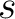 is a linear combination of the spin weighted harmonics
is a linear combination of the spin weighted harmonics
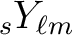
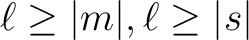 ,
and is such that
,
and is such that
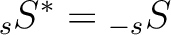 .
.
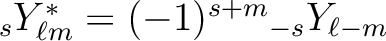 and therefore
and therefore
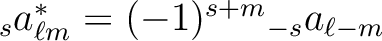 .
The two (real) input maps for map2alm_spin* are defined respectively as
.
The two (real) input maps for map2alm_spin* are defined respectively as
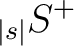 |
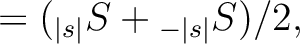 |
(13) |
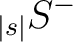 |
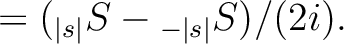 |
(14) |
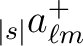 |
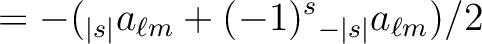 |
(15) |
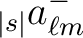 |
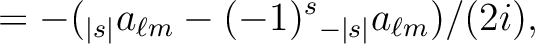 |
(16) |
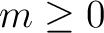 , knowing that, just as for spin 0 maps, the
coefficients for
, knowing that, just as for spin 0 maps, the
coefficients for 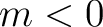 are given by
are given by
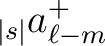 |
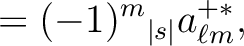 |
(17) |
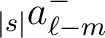 |
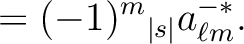 |
(18) |
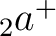 ,
, 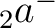 ,
, 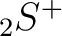 and
and 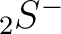 match HEALPix polarization
match HEALPix polarization
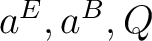 and
and 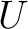 respectively. However, for
respectively. However, for
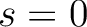 ,
,
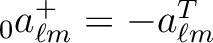 ,
,
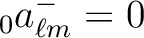 ,
,
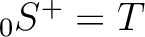 ,
,
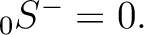
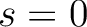 , it is
highly recommended, and much more memory-efficient, to use directly the routine map2alm, rather then setting spin
, it is
highly recommended, and much more memory-efficient, to use directly the routine map2alm, rather then setting spin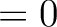 in map2alm_spin*.
Location in HEALPix directory tree: src/f90/mod/alm_tools.F90
in map2alm_spin*.
Location in HEALPix directory tree: src/f90/mod/alm_tools.F90
call map2alm_spin*( nsmax, nlmax, nmmax, spin, map, alm[, zbounds=, w8ring_TQU=] )
Analyses spin 5 and -5 maps. The maps have anof 256, and the analysis is performed up to 512 in
and
. The resulting
coefficients for are returned in alm.
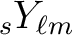 recursion
recursion
 value.
value.
Version 3.83, 2024-11-13