Previous: map2alm* Up: HEALPix Fortran90 Subroutines Overview Next: map2alm_spin* Top: Main Page
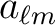 coefficients for temperature (and polarisation) up to a specified
multipole, and use precomputed harmonics if those
are provided, but it also can also perform an iterative (Jacobi) determination of the
coefficients for temperature (and polarisation) up to a specified
multipole, and use precomputed harmonics if those
are provided, but it also can also perform an iterative (Jacobi) determination of the
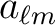 , and
apply a pixel mask if one is provided.
, and
apply a pixel mask if one is provided.
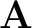 and
and
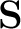 the
analysis (map2alm) and
synthesis (alm2map)
operators and
the
analysis (map2alm) and
synthesis (alm2map)
operators and
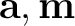 and
and
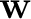 , the
, the
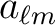 , map and pixel mask vectors, the
Jacobi iterative process reads
, map and pixel mask vectors, the
Jacobi iterative process reads
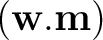 and the current residual map
and the current residual map
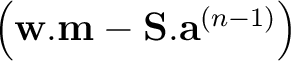 is printed out, with the latter expected
to get smaller and smaller as
is printed out, with the latter expected
to get smaller and smaller as 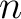 increases.
increases.
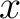 has the usual definition
has the usual definition
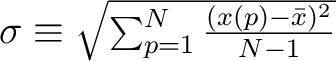 , where the mean is
, where the mean is
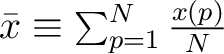 , and the index
, and the index 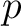 runs over all pixels.
runs over all pixels.
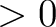 was used in conjonction with a
mask
and/or a restrictive
zbounds,
with a magnitude that depended on each of those factors and was larger for non-boolean masks (ie,
was used in conjonction with a
mask
and/or a restrictive
zbounds,
with a magnitude that depended on each of those factors and was larger for non-boolean masks (ie,
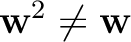 ).
To assess the impact of this bug on previous results, the old implementation remains available in
map2alm_iterative_old).
The result was correct when the mask (if any) was applied to the map prior to the
map2alm_iterative calling, or when no iteration was requested.
).
To assess the impact of this bug on previous results, the old implementation remains available in
map2alm_iterative_old).
The result was correct when the mask (if any) was applied to the map prior to the
map2alm_iterative calling, or when no iteration was requested.
call map2alm_iterative( nsmax, nlmax, nmmax, iter_order, map_TQU, alm_TGC[, zbounds, w8ring_TQU, plm, mask] )
| name & dimensionality | kind | in/out | description |
|---|---|---|---|
| nsmax | I4B | IN | the
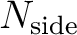 value of the map to analyse. value of the map to analyse. |
| nlmax | I4B | IN | the maximum 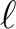 value ( value (
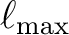 ) for the analysis. ) for the analysis. |
| nmmax | I4B | IN | the maximum 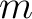 value for the analysis. value for the analysis. |
| iter_order | I4B | IN | the order of Jacobi iteration. Increasing that order
improves the accuracy of the final
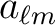 but increases the computation time but increases the computation time
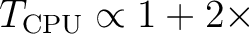 iter_order.
iter_order iter_order.
iter_order 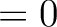 is a straight analysis, while iter_order is a straight analysis, while iter_order 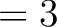 is usually a
good compromise. is usually a
good compromise. |
| map_TQU(0:12*nsmax**2-1, 1:p) | SP/ DP | INOUT | input map. 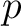 is 1 or 3
depending if temperature (T) only or temperature and polarisation (T, Q, U) are
to be analysed. It will be altered on output if a mask is provided and/or if iter_order is 1 or 3
depending if temperature (T) only or temperature and polarisation (T, Q, U) are
to be analysed. It will be altered on output if a mask is provided and/or if iter_order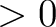 and zbounds is provided. and zbounds is provided. |
| alm_TGC(1:p, 0:nlmax, 0:nmmax) | SPC/ DPC | OUT | The
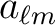 values output
from the analysis. values output
from the analysis.
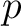 is 1 or 3 depending on whether polarisation is included or not. In the former
case, the first index is (1,2,3) corresponding to (T,E,B). is 1 or 3 depending on whether polarisation is included or not. In the former
case, the first index is (1,2,3) corresponding to (T,E,B). |
| zbounds(1:2), OPTIONAL | DP | IN | section of the map on which to perform the
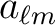 analysis, expressed in terms of
analysis, expressed in terms of
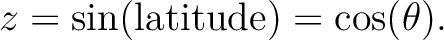 If zbounds(1) If zbounds(1)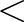 zbounds(2), it is
performed on the strip zbounds(1) zbounds(2), it is
performed on the strip zbounds(1)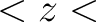 zbounds(2); if not,
it is performed outside the strip
zbounds(2) zbounds(2); if not,
it is performed outside the strip
zbounds(2)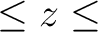 zbounds(1). If absent, the whole map is processed. zbounds(1). If absent, the whole map is processed.
|
Analyses temperature and polarisation signals in the first 10000 pixels of map (as determined by mask). The map has anof 256, and the analysis is supposed to be performed up to 512 in
and
. The resulting
coefficients for temperature and polarisation are returned in alm. Uniform weights are assumed. In order to improve the
accuracy, 2 Jacobi iterations are performed.
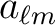 coefficients
computed by map2alm_iterative into a FITS file
coefficients
computed by map2alm_iterative into a FITS file
Version 3.83, 2024-11-13