Previous: Discretisation of Functions on the Sphere Up: The HEALPix Primer Next: The HEALPix Software Package Top: Main Page
HEALPix is a genuinely curvilinear partition of the sphere into exactly equal area quadrilaterals of varying shape. The base-resolution comprises twelve pixels in three rings around the poles and equator.
The resolution of the grid is expressed by the parameter
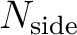 which defines the number
of divisions along the side of a base-resolution pixel that is needed to reach a desired
high-resolution partition.
which defines the number
of divisions along the side of a base-resolution pixel that is needed to reach a desired
high-resolution partition.
All pixel centers are placed on
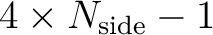 rings of constant latitude,
and are equidistant in azimuth
(on each ring). All iso-latitude rings located between the upper and lower corners of
the equatorial base-resolution pixels, the equatorial zone,
are divided into the same number of pixels:
rings of constant latitude,
and are equidistant in azimuth
(on each ring). All iso-latitude rings located between the upper and lower corners of
the equatorial base-resolution pixels, the equatorial zone,
are divided into the same number of pixels:
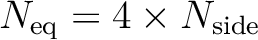 . The remaining rings are located within the
polar cap regions and contain a varying number of pixels, increasing
from ring to ring with increasing distance
from the poles by one pixel within each quadrant.
. The remaining rings are located within the
polar cap regions and contain a varying number of pixels, increasing
from ring to ring with increasing distance
from the poles by one pixel within each quadrant.
Pixel boundaries are non-geodesic and take the very simple
forms
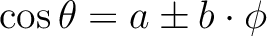 in the equatorial zone
(
in the equatorial zone
(
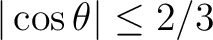 ),
and
),
and
 , or
, or
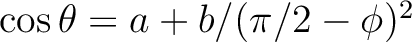 ,
in the polar caps, with
,
in the polar caps, with 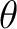 being the co-latitude, and
being the co-latitude, and 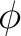 the longitude.
This allows one to explicitly check by simple analytical integration the
exact area equality among pixels (Górski et al., 2005),
and to compute efficiently more complex objects,
e.g. the Fourier transforms of individual pixels.
the longitude.
This allows one to explicitly check by simple analytical integration the
exact area equality among pixels (Górski et al., 2005),
and to compute efficiently more complex objects,
e.g. the Fourier transforms of individual pixels.
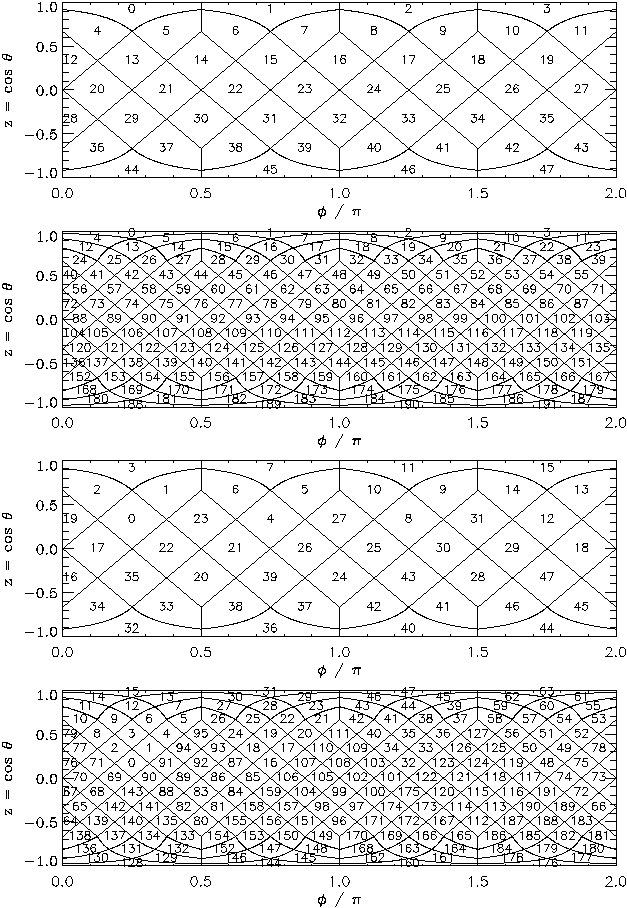 |
First, in the RING scheme, one can simply count the pixels moving down from the north to the south pole along each iso-latitude ring. It is in the RING scheme that Fourier transforms with spherical harmonics are easy to implement.
Second, in the NESTED scheme, one can arrange the pixel indices
in twelve tree structures, corresponding to base-resolution pixels.
Each of those is organised as shown in Fig. 1. This can easily be implemented
since, due to the simple
description of pixel boundaries, the analytical mapping of the HEALPix
base-resolution elements (curvilinear
quadrilaterals) into a [0,1] [0,1] square exists.
This tree structure allows one to implement efficiently all
applications involving nearest-neighbour searches
(Wandelt, Hivon & Górski, 1998),
and also allows for an immediate
construction of the fast Haar wavelet transform on HEALPix.
[0,1] square exists.
This tree structure allows one to implement efficiently all
applications involving nearest-neighbour searches
(Wandelt, Hivon & Górski, 1998),
and also allows for an immediate
construction of the fast Haar wavelet transform on HEALPix.
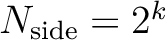 (where
(where  is a integer sometimes called 'order'),
and its index
is a integer sometimes called 'order'),
and its index 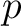 lying in
lying in
![$[0, 12N_{\mathrm{side}}^2-1]$](intro_img24.png) .
Since some applications require to process simultaneously pixels of different resolutions, it is possible
to merge the resolution
.
Since some applications require to process simultaneously pixels of different resolutions, it is possible
to merge the resolution
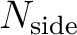 and index
and index 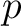 into a single unique number
into a single unique number 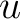 so that all pixels with
so that all pixels with
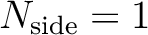 have the unique indices 4 to 15,
those with
have the unique indices 4 to 15,
those with
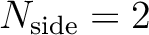 are in the range 16 to 63, and so on (Reinecke & Hivon, 2015),
thus simplifying the handling of data with heteregenous
are in the range 16 to 63, and so on (Reinecke & Hivon, 2015),
thus simplifying the handling of data with heteregenous
 .
Splitting the unique index
.
Splitting the unique index 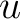 into its original
into its original
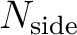 and
and 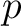 is as simple as
giving immediate access to the usual pixel based tools.
is as simple as
giving immediate access to the usual pixel based tools.
This unique indexing could in principle be applied to both the RING and NESTED schemes,
even though the latter appears more relevant for a hierarchical description
of data with variable resolutions: since, as noted previously, a pixel with NESTED index 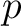 at resolution
at resolution
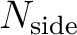 is subdivided in four pixels with index
is subdivided in four pixels with index
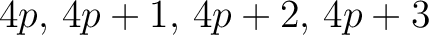 at resolution
at resolution
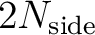 , Eq. (1) shows that
a pixel with Nested-based unique identifier
, Eq. (1) shows that
a pixel with Nested-based unique identifier 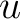 is subdivided in four smaller pixels
whose unique identifiers are
is subdivided in four smaller pixels
whose unique identifiers are
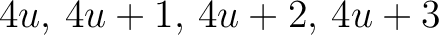 .
This Nested-based Unique identification is for instance the basis of the NUNIQ storage scheme used for Multi-Order Coverage map (MOC) description of astronomical datasets proposed for virtual observatories (Boch et al., 2014).
.
This Nested-based Unique identification is for instance the basis of the NUNIQ storage scheme used for Multi-Order Coverage map (MOC) description of astronomical datasets proposed for virtual observatories (Boch et al., 2014).
Routines implementing Eqs (1) and (2, 3) in various languages have been available since release 3.30.
Version 3.83, 2024-11-13