Previous: HEALPix conventions Up: The HEALPix Primer Next: A Comment on the Random Number Top: Main Page
A pixelated signal 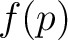 is the average within each pixel
is the average within each pixel 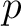 (with surface
area
(with surface
area
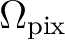 ) of the underlying signal
) of the underlying signal
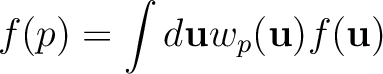 |
(30) |
 is equal to
is equal to
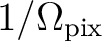 within the pixel, and equal to 0 outside, so
that
within the pixel, and equal to 0 outside, so
that
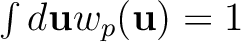 .
Eq. (4) then becomes
.
Eq. (4) then becomes
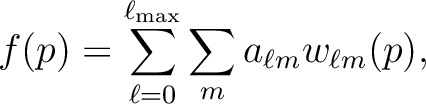 |
(31) |
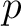 .
.
However, complete analysis of a pixelated map with the exact
 defined above would be computationally intractable (because of azimutal
variation of pixel shape over the polar caps of the HEALPix grid),
and some simplifying asumptions have to be
made. If the pixel is small compared to the signal correlation length
(determined by the beam size), the exact structure of the pixel can be ignored
in the subsequent analysis and we can assume
defined above would be computationally intractable (because of azimutal
variation of pixel shape over the polar caps of the HEALPix grid),
and some simplifying asumptions have to be
made. If the pixel is small compared to the signal correlation length
(determined by the beam size), the exact structure of the pixel can be ignored
in the subsequent analysis and we can assume
 |
(33) |
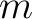 -averaged window function
which is independent of the pixel location on the sky.
-averaged window function
which is independent of the pixel location on the sky.
If we assume all the pixels to be identical, the power spectrum of the
pixelated map,
 , is related to the hypothetical unpixelated
one,
, is related to the hypothetical unpixelated
one,
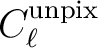 , by
, by
 is defined as
This function is provided with the HEALPix package for
is defined as
This function is provided with the HEALPix package for
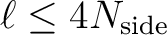 for each
resolution parameter
for each
resolution parameter
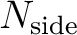 .
.
The pixel window functions are now available for both temperature and polarization.
For
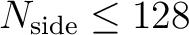 , those window functions are computed exactly using
Eqs. (34) and (36). For
, those window functions are computed exactly using
Eqs. (34) and (36). For
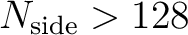 the
calculations are too costly to be done exactly at all
the
calculations are too costly to be done exactly at all  . The temperature
windows are
extrapolated from the case
. The temperature
windows are
extrapolated from the case
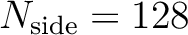 assuming a scaling in
assuming a scaling in 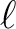 similar
to the one exhibited by the window of a tophat pixel. The polarization
windows are assumed to be proportional to those for temperature, with a
proportionality factor given by the exact calculation of
similar
to the one exhibited by the window of a tophat pixel. The polarization
windows are assumed to be proportional to those for temperature, with a
proportionality factor given by the exact calculation of  at low
at low
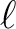 .
.
Because of a change of the extrapolation scheme used, the temperature window
functions provided with HEALPix 1.2 and higher for
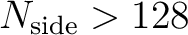 are slighty different from those
provided with HEALPix 1.1. For a given
are slighty different from those
provided with HEALPix 1.1. For a given
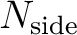 , the relative difference
increases almost linearly with
, the relative difference
increases almost linearly with 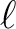 , and is of the order of
, and is of the order of
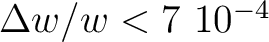 at
at
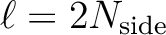 and
and
 at
at
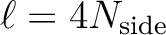 .
.
Version 3.83, 2024-11-13